Decay Equations

The decay equation of a light source is defined by the type of light which is considered and by some parameters:

• Physically correct lights have no customizable decay equation. The decay result of the light source itself.

• Non physically correct lights may use several decay equations, that can be taylored to the application needs.

Physical Lights Intensity Decay

The decay of a physical light (RED::IPhysicalLightShape, RED::ISunLightShape, RED::ISkyLightShape) results of the visible solid angle of the light from the shaded point considered. This produces a natural quadratic decay of the intensity of the light source as the shaded point goes away:

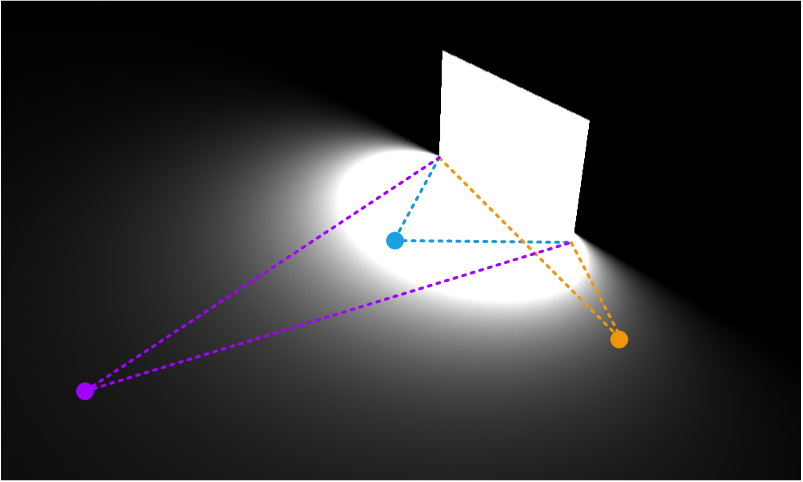
Decay resulting of a physical light visible solid angle

This schema illustrates (in 2D to make the picture simpler) the diminishing solid angle of the light source visible from a shaded point as long as this point goes either far away from the light source (violet point) or to the side of it (orange point), compared to the central point (in blue).

Therefore, the decay equation of a physical light source is the direct result of its geometry, and not of anything else.

Non Physical Lights Intensity Decay

The following decay equations are available for lights that can leverage them. These equations are using an array of 7 floating point values, that are set through the RED::ILightShape::SetAttenuation call or in light typing calls (example: RED::ILightShape::SetPointLight). In the figures below, we call them ATT[x]:

Decay Equation	Details
RED::ATN_NONE	Intensity is 1 for the entire light source effect area.
RED::ATN_LINEAR	Intensity linearly decreases as the lit point moves away from the light. INTENSITY = IMAX / DISTANCE; where IMAX = ATT[0].
RED::ATN_QUADRATIC	Intensity decreases using a quadratic equation as the lit point moves away from the light. INTENSITY = IMAX / POW(DISTANCE,2); where IMAX = ATT[0].
RED::ATN_CUBIC	Intensity decreases using a cubic equation as the lit point moves away from the light. INTENSITY = IMAX / POW(DISTANCE,3); where IMAX = ATT[0].
RED::ATN_DMAX2	Intensity decreases using a ratio between the current distance to the lit point and a reference distance. INTENSITY = 1 - POW(DISTANCE / DMAX,2); where DMAX = ATT[0].
RED::ATN_LINQUA	Intensity uses a 2nd order equation: INTENSITY = 1 / ( 1 + KLIN * DISTANCE + KQUA * DISTANCE); where ATT[0] = KLIN and ATT[1] = KQUA.
RED::ATN_N3DSMAX	3DSMax decay. Near and far attenuation distances can be used, and the intensity does not vary with the distance besides that. INTENSITY = 1.
RED::ATN_L3DSMAX	3DSMax decay. Near and far attenuation distances can be used, and the intensity decreases using the following equation: INTENSITY = min( 1, DREF / D ); where DREF = ATT[0].
RED::ATN_Q3DSMAX	3DSMax decay. Near and far attenuation distances can be used, and the intensity decreases using the following equation: INTENSITY = min( 1, POW(DREF / D,2) ); where DREF = ATT[0].

RED::ATN_N3DSMAX, RED::ATN_L3DSMAX and RED::ATN_Q3DSMAX are Autodesk / 3ds Max software specific equations:

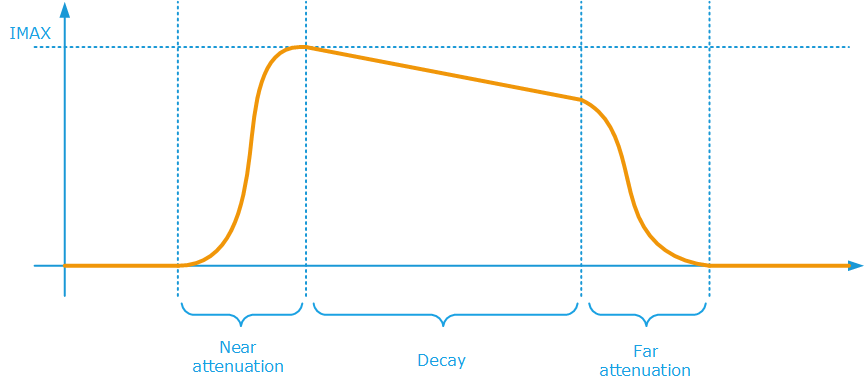
Autodesk 3ds Max specific decay equations

We have:

• ATT[0] = IMAX.

• ATT[1] = VALUE IGNORED.

• ATT[2] = NEAR ATTENUATION START.

• ATT[3] = NEAR ATTENUATION STOP.

• ATT[4] = FAR ATTENUATION START.

• ATT[5] = FAR ATTENUATION STOP.

• ATT[6] = EXTRA INTENSITY SCALE (this value is a multiplier applied to the effect area of the light source, if we have no far attenuation enabled).

NEAR and FAR attenuations are enabled only if ATT[2] and / or ATT[4] are strictly positive values. Otherwise, the decay starts at 0 distance, and ends up at the effect area of the light source. Please note that in the near and far attenuation regions of the decay curve, the 3*(d*d) - 2*(d*d*d) equation is used, where d is the relative distance within the considered attenuation region. Please also note that the RED::ATN_LINEAR, RED::ATN_QUADRATIC, and RED::ATN_CUBIC equations are the usual equations found in Autodesk / Maya.